|
|
     |
Eleverne på Tornbjerg Gymnasium synes at sætte pris på en enkelt fadøl i "Jazz-ekspresen" om fredagen, inden de kører hjem efter en gård skoleuge.
Tradition byder, at der serveres øl fra det lokale Albani-bryggeri; men måske foretrækker nogle af leverne i virkeligheden mere eksotiske ølsorter som f.eks. Hof eller Tuborg.
For at opklare dette problem har opinionsinstituttet "Obscura" gennemført en meningsmåling i "Jazz-ekspressen". De noget overraskende resultater af undersøgelsen er anført neden for:
Hvor mange % kan lide både Odense og Hof, men ikke Tuborg?
I deres fritid finder elever fra Tognbjerg Gymnasium undertiden fornøjelse i at opsøge et af de efterhånden mange etablissementer i den indre by, hvor man kan spille Pool. Her kan de fordrive tiden på behageligste måde, mens de ved billard-bordret studerer fysikkens elementære lovmæssigheder som energi- og impulsbevarelse. Det er jo i enhver forstand en trøstende tanke, at selv de mest komplicerede "trick-shots" er underlagt disse simple love.
Nedenstående lille problem stammer fra et sådant besøg:
Et billardbord er 9 enheder langt og 7 enheder bredt, og diameteren af billardkuglen svare nøjagtigt til størrelsen af hjørnehullerne. Der er ingen gnidning på bordret og banderne er fuldstendigt elastiske. Desuden er refleksionsloven opfyldt, således at indfaldsvinkel = udfaldsvinkel, hver gang billardkuglen rammer banden.
En billardkugle skydes ud fra det nederste venstre huld i en vinkel på 45° i forhold til hver af kanterne.
Det er velkendt, at eleverne på Tornbjerg Gymnasium er meget opmærksomme på deres fodtøj. Selvom vejret indbyder mere til sandaler eller gummistøvler, vælger eleverne sædvanligvis at bære moderigtige snøresko.
Da disse sko forhandles til ret pebrede priser og SU'en som bekendt kun kan bruges én gang, gælder det om at spare, hvor man kan. I dette tilfælde kan der spares - ved forbruget af snørebånd.
Nedenstående lille problem viser, hvordan man ved et intelligent valg af snøringsmetode kan minimere udgifterne til snørebånd. Hvem ved, hvor mange penge kan det blive til over et helt liv?
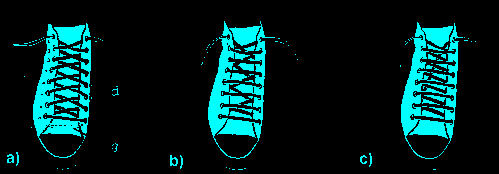
Snørebånd kan bindes efter tre principper: a) Den almindelige "zig-zag" -metode, der er den etteste at lære og som børn altid anvender, b) "lige-over" -metoden, der er lidt mere avanceret og ikke så lidt mere elegant. Endelig er der c) "skobutik" -metoden, som er den snøringmetode, skoene fødes med i butikken.
Hvilken af disse metoder kræver mindst snørebånd?
For at løse dette problem indfører vi følgende notation:
n = antal rækker snørebåndshuller i skoen
d = afstanden mellem to rækker snørebpndshuller
g = afstanden mellem højre og venstre størebåndshul i en række.
Flere gange om året indbyder Tornbjerg Gymnasiums elevforening "Miracules" til fest på gymnasiet. Eleverne hilser den slags initiativer velkomen og møder altid talstærkt op.
Ved sådanne lejligheder kan man observere et usædvanligt fænomen. Den del af kantinen, hvor der danses, fyldes op til bristepunktet af dansende gymnasieelever, så man kun med største besvær kan mase sig igennem området. Udenfor dansegulvet, hvor folk står og hænger i mindre grupper, er der derimod så god plads, at man kan bevæge sig i et raskt og ubesværet tempo.
Dette forhold er vigtigt i forstøelsen af nedenstående principielle problem, der rent intuitivt løses mange gange til hver Miracules-fest:
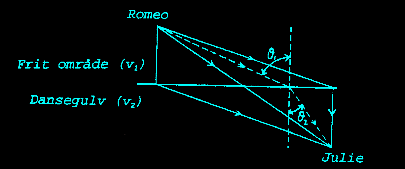
Den lokale Romeo har placeret sig uden for dansegulvet for at nyde at øjebliks ro og vederkvægelse. Pludselig får han øje på sin Julie midt ude på dansegulvet i armene på en Leonardo di Capprio-lignende type. Det antages, at der herved opstår en konfliktsituation......
Romeo's principielle problem er nu, at han skal nå julie på den mindst mulige tid under hensyntagen til, at han udenfor dansegulvet kan bevæge sig med en høj hastighed v1, mens han på dansegulvet kun kan bevæge sig med en lav hastighed v2. Hvilken retning skal han vælge?
Vis, at når Romeo vælger den hurtigste vej (den stiplede linie på figuren) bestemt ved vinklerne 
1 og 2 med normalen på dansefronten, så gælder følgende relation:
1) * v2 = sin(2) * v1